1.线性回归

对包含$d$个属性描述的数据${\bf{x}} = \{ {x_1},{x_2},...,{x_d}\}$，建立一个加权线性模型，$f({\bf{x}}) = {\omega _1}{x_1} + {\omega _2}{x_2} + ... + {\omega _d}{x_d} + b$，尽可能预测地准确对应的标签值$y$，各权重$\omega$直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性。

 

我们先考虑最简单的情况，$d=1$。线性回归试图学得$f(x_i) = {\omega } {x_i}+ b$，使得$f(x_i) \simeq {y_i}$。如何衡量这两个之间的差别呢？均方误差是回归任务中最常用的性能度量，因此我们可以试图让均方误差最小化，

\[\begin{array}{*{c}}

{({\omega ^*},{b^*}) = \mathop {\arg \min }\limits_{\omega ,b} \sum\limits_{i = 1}^m {

{

{\left( {f({x_i}) - {y_i}} \right)}^2}} }\\

{ = \mathop {\arg \min }\limits_{\omega ,b} \sum\limits_{i = 1}^m {

{

{\left( {

{\omega ^T}{x_i} + b - {y_i}} \right)}^2}} }

\end{array}\]

均方误差有非常好的几何意义，对应了欧氏距离。基于均方误差最小化来进行求解的方法成为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

 

 

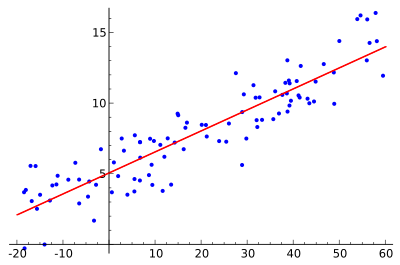
求解$\omega$和$b$使$E(\omega ,b) = \sum\limits_{i = 1}^m {

{

{\left( {

{\omega }{x_i} + b - {y_i}} \right)}^2}} $最小化的过程，称之为线性回归模型的最小二乘“参数估计”。由于$E(\omega ,b) $是凸函数，令$\omega$和$b$的偏导为零，可以求其最优解的闭式解。 

\[\begin{array}{l}

\frac{

{\partial E(\omega ,b)}}{

{\partial \omega }} = 2\sum\limits_{i = 1}^m {\left( {\omega {x_i} + b - {y_i}} \right){x_i} = 0} \\

\frac{

{\partial E(\omega ,b)}}{

{\partial b}} = 2\sum\limits_{i = 1}^m {\left( {\omega {x_i} + b - {y_i}} \right)} = 0

\end{array}\]

\[\begin{array}{l}

\omega \sum\limits_i^m {x_i^2} + b\sum\limits_i^m {

{x_i}} - \sum\limits_i^m {

{y_i}{x_i}} = 0\\

\omega \sum\limits_i^m {

{x_i}} + mb - \sum\limits_i^m {

{y_i}} = 0

\end{array}\]

\[\begin{array}{l}

\omega = \frac{

{\sum\limits_i^m {

{y_i}} ({x_i} - \frac{1}{m}\sum\limits_i^m {

{x_i}} )}}{

{\sum\limits_i^m {x_i^2} - \frac{1}{m}{

{(\sum\limits_i^m {

{x_i}} )}^2}}}\\

b = \frac{1}{m}\sum\limits_i^m {({y_i} - \omega {x_i})}

\end{array}\]

 

更一般的情况，针对数据集$D = \{ ({

{\bf{x}}_1},{y_1}),({

{\bf{x}}_2},{y_2}),...,({

{\bf{x}}_m},{y_m})\} $，其中${

{\bf{x}}_i} = \{ {x_{i1}},{x_{i2}},...,{x_{id}}\} $，包含d维特征。试图学得$f({

{\bf{x}}_i}) = {

{\bf{\omega }}^T}{

{\bf{x}}_i} + b$，使得$f({\bf{x}_i}) \simeq {y_i}$，这称之为“多元线性回归”。

类似用最小二乘法求得${\bf{\hat \omega }} = ({\bf{\omega }};b)$最优解的闭式解，相应的数据集表示为，

\[{\bf{X}} = \left( {\begin{array}{*{20}{c}}

{

{\bf{x}}_{\bf{1}}^{\bf{T}}}&1\\

{

{\bf{x}}_{\bf{2}}^{\bf{T}}}&1\\

{...}&1\\

{

{\bf{x}}_{\bf{m}}^{\bf{T}}}&1

\end{array}} \right)\]

\[{\bf{y}} = ({y_1};{y_2};...{y_m})\]

令优化目标值${E_{

{\bf{\hat \omega }}}} = {({\bf{y}} - {\bf{X\hat \omega }})^T}({\bf{y}} - {\bf{X\hat \omega }})$，求偏导为0，得$\bf{\hat \omega }$最优解的闭式解，

\[{

{

{\bf{\hat \omega }}}^*} = \mathop {\arg \min }\limits_{

{\bf{\hat \omega }}} {({\bf{y}} - {\bf{X\hat \omega }})^T}({\bf{y}} - {\bf{X\hat \omega }})\]

\[\frac{

{\partial {E_{

{\bf{\hat \omega }}}}}}{

{

{\bf{\hat \omega }}}} = \frac{

{\partial {

{({\bf{y}} - {\bf{X\hat \omega }})}^T}}}{

{

{\bf{\hat \omega }}}}({\bf{y}} - {\bf{X\hat \omega }}) + {({\bf{y}} - {\bf{X\hat \omega }})^T}\frac{

{\partial ({\bf{y}} - {\bf{X\hat \omega }})}}{

{

{\bf{\hat \omega }}}}\]

\[ =  - {

{\bf{X}}^{\bf{T}}}({\bf{y}} - {\bf{X\hat \omega }}) - {({\bf{y}} - {\bf{X\hat \omega }})^T}{\bf{X}}\]

（标量的转置等于其本身）

\[ = 2{

{\bf{X}}^{\bf{T}}}({\bf{X\hat \omega }} - {\bf{y}})\]

但涉及矩阵逆计算，要复杂很多，下面做一个简单的讨论。当${

{\bf{X}}^{\bf{T}}}{\bf{X}}$为满秩矩阵或正定矩阵时，可求其逆矩阵，

\[{\bf{\hat \omega }} = {({

{\bf{X}}^{\bf{T}}}{\bf{X}})^{ - 1}}{

{\bf{X}}^{\bf{T}}}{\bf{y}}\]

多元线性回归模型为，

 \[f({

{

{\bf{\hat x}}}_i}) = {\bf{\hat x}}_i^T{({

{\bf{X}}^{\bf{T}}}{\bf{X}})^{ - 1}}{

{\bf{X}}^{\bf{T}}}{\bf{y}}\]

然而，现实任务中然而，现实任务中 xTx 往往不是满秩矩阵.例如在许多任务中我们会遇到大量的变量，其数目甚至超过样例数，导致 X 的列数多于行数 ， xTx 显然不满秩。此时可解出多个解， 它们都能使均方误差最小化。选择哪一个解作为输出 ，将由学习算法的归纳偏好决定， 常见的做法是引入正则化 (regularization)项.

 

 

线性回归模型的一般形式为：

\[y = {

{\bf{\omega }}^T}{\bf{x}} + b\]

如果我们的数据是成指数变化的，那么可以把线性回归模型扩展为：

\[\ln y = {

{\bf{\omega }}^T}{\bf{x}} + b\]

更一般的，考虑单调可微函数$g(\bullet)$，将线性回归模型的预测值与真实标记联系起来，那么线性回归模型扩展为：

\[y = {g^{ - 1}}({

{\bf{\omega }}^T}{\bf{x}} + b)\]

2. logistic回归

那怎么把线性回归模型扩展到分类模型中呢，找一个单调可微函数，将线性回归模型的预测值与真实类别联系起来。

考虑二分类问题，单位阶跃函数是理想的分类函数，若预测值大于0则为{1}正类，小于0则为{0}负类，等于0则可任意判别。但是这样的阶跃函数不连续，不是可微的。因此我们利用对数几率函数（logistic function）来近似单位阶跃函数。

\[y = \frac{1}{

{1 + {e^{ - z}}}}\]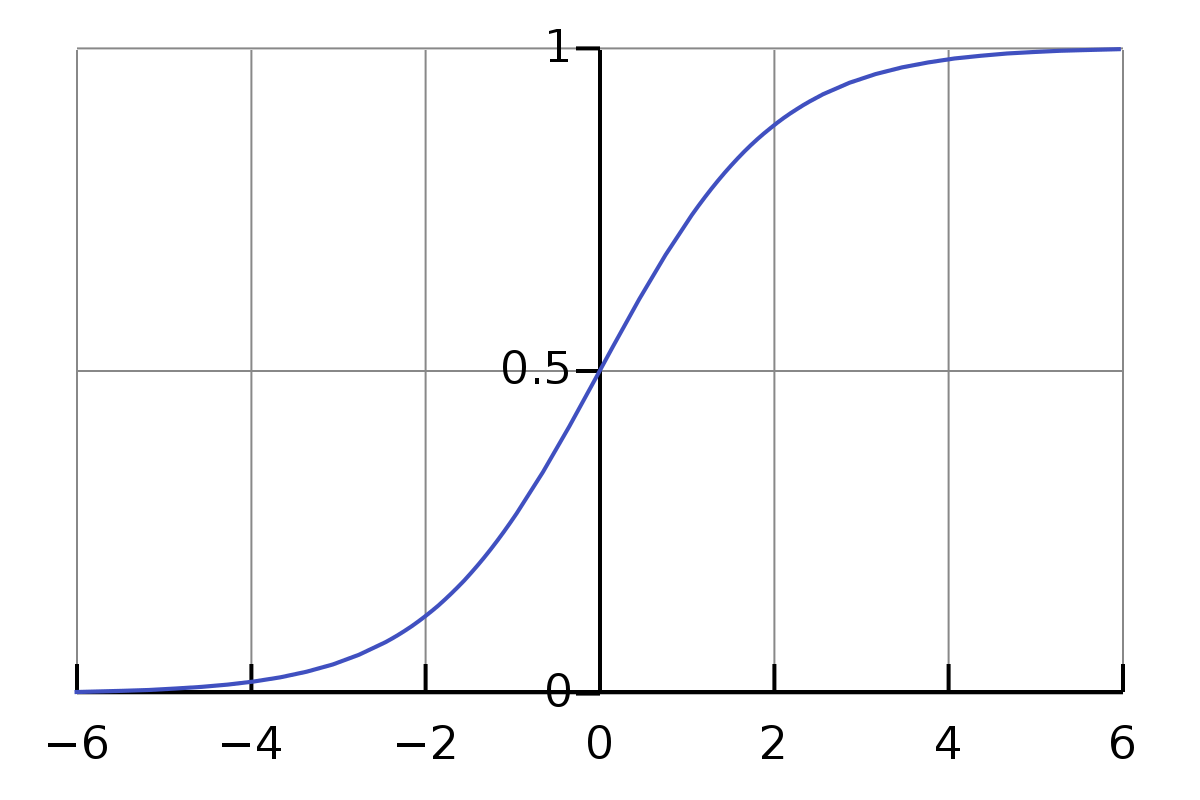

 

将z值转化成一个接近于0或1的y值。

\[\ln \frac{y}{

{1 - y}} = {

{\bf{\omega }}^T}{\bf{x}} + b\]

 \[\ln \frac{

{p(y = 1|x)}}{

{p(y = 0|x)}} = {

{\bf{\omega }}^T}{\bf{x}} + b\]

该模型是在用线性回归模型的预测值去逼近真实标记的对数（$\ln$）几率（$\frac{y}{1 - y}$），其对应的模型成为“logistic回归”。

视y为类后验概率估计$p(y=1|x)$，有：

\[y = p(y = 1|x) = \frac{1}{

{1 + {e^{ - {

{\bf{\omega }}^T}{\bf{x}} - b}}}}\]

\[y = p(y = 1|x) = \frac{1}{

{1 + {e^{  {

{\bf{\omega }}^T}{\bf{x}} + b}}}}\]

 

极大似然估计的思想为：对于所有的抽样样本，使它们联合概率${p({y_i}|{

{\bf{x}}_i};{\bf{w}},b)}$达到最大的系数便是统计模型最优的系数。

给定数据集D，因为对数函数ln（x）是单调增函数，且可以把乘除转换成加减，利于数学计算，所以logistic回归模型最大化“对数似然”，

\[l({\bf{w}},b) = \sum\limits_{i = 1}^m {\ln p({y_i}|{

{\bf{x}}_i};{\bf{w}},b)} \]

为了便于讨论，令$\bf{\beta}= ({\bf{w}};b)$，$\widehat{\bf{x}}= (\bf{x};1)$，对数似然等价为最小化

\[l({\bf{\beta }}) = \sum\limits_{i = 1}^m {( - {y_i}{

{\bf{\beta }}^T}{

{\widehat {\bf{x}}}_i} + \ln (1 + {e^{

{

{\bf{\beta }}^T}{

{\widehat {\bf{x}}}_i}}}))} \]

可根据经典数值优化算法如梯度下降法等求得其$\bf{\beta }$的最优解，

\[{

{\bf{\beta }}^*} = \mathop {\arg \min }\limits_{\bf{\beta }} l({\bf{\beta }})\]

 

---

logistic回归算法

输入：训练集$D = \{ ({

{\bf{x}}_1},{y_1}),({

{\bf{x}}_2},{y_2}),...,({

{\bf{x}}_m},{y_m})\} $；

           学习率$\alpha$;

　　　终止条件$\varepsilon$.

过程：

1：令$\bf{\beta}= ({\bf{w}};b)$，$\widehat{\bf{x}}= (\bf{x};1)$

2：针对$l({\bf{\beta }}) = \sum\limits_{i = 1}^m {( - {y_i}{

{\bf{\beta }}^T}{

{\widehat {\bf{x}}}_i} + \ln (1 + {e^{

{

{\bf{\beta }}^T}{

{\widehat {\bf{x}}}_i}}}))} $

      利用随机梯度下降法求最优解${

{\bf{\beta }}^*} = \mathop {\arg \min }\limits_{\bf{\beta }} l({\bf{\beta }})$

3：初始化$\bf{\beta}_0$

4：repeat

5：从训练集D中随机挑选一个数据${\bf{x}_i}, y_i$

6：以学习率$\alpha$的速度朝梯度下降的方向更新参数$\bf{\beta}$

7：end for

8：until $\Delta {\bf{\beta }} \le \varepsilon $

输出：logistic回归模型参数$\bf{w},b$

---

 

参考：

机器学习西瓜书 周志华